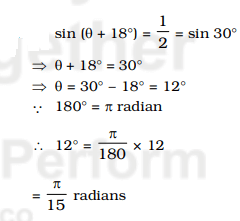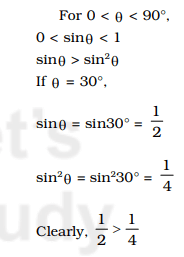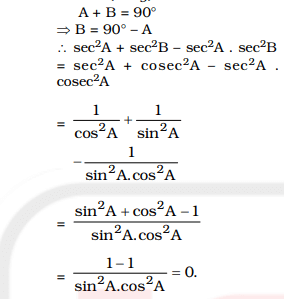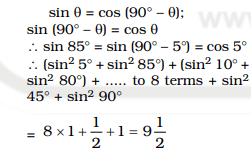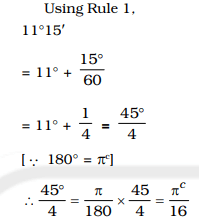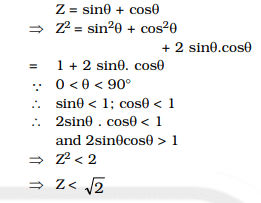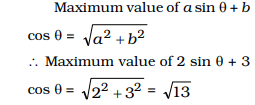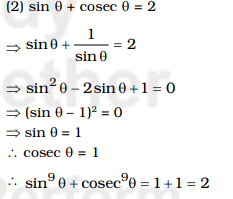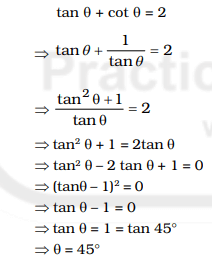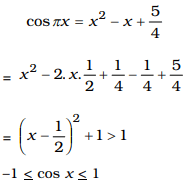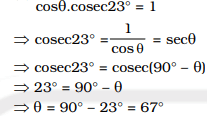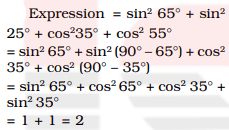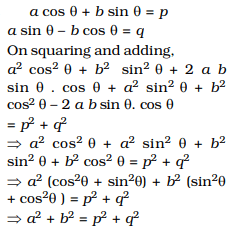Trigonometry MCQ Quiz

A trigonometry is a unit of mathematics that studies relationships. Test your trigonometry calculation with particular and important questions of side lengths and angles of triangles.

Here you can solve and practice Trigonometry questions.

Complete Trigonometry Quiz

Question 1. The degree measure of 1 radian (taking π =22/7 ) is 

(A) 57°16’22” (approx.)

(B) 57°32’16” (approx.)

(C) 57°61’22” (approx.)

(D) 57°22’16” (approx.)

Question 2. The circular measure of the included angle formed by the hour hand and minute hand of a clock at 3 p.m. will be 

(A) π/3

(B) π/4

(C) π/2

(D) 5π/12

Question 3. The value of tan 4°.tan 43°.tan 47°.tan 86° is 

(A) 3

(B) 4

(C) 2

(D) 1

Question 4. If cos x + cos y = 2, the value of sin x + sin y is

(A) 2

(B) 0

(C) -1

(D) 1

Question 5. The value of tan1°tan2° tan3°……. tan89° is :

(A) 0

(B) √3

(C) 1

(D) 1/√3

Question 6. The circular measure of an angle of an isosceles triangle is 5π/9.Circular measure of one of the other angles must be

(A) 5π/9

(B) 5π/18

(C) 4π/9

(D) 2π/9

Question 7. If x, y are acute angles, 0 < x +y < 90° and sin (2x – 20°) = cos (2y + 20°), then the value of tan (x + y) is : 

(A) √3/2

(B) 1√3

(C) 1

(D) √3

Question 8. If Θ is an acute angle and sin (Θ +18°) =1/2, then the value of q in circular measure is : 

(A) π/15 radian

(B) π/12 radian

(C) 2π/5 radian

(D) 3π/13 radian

Question 9. Which of the following relations is correct for 0 < Θ < 90° ?

(A) sinΘ = cosecΘ

(B) sinΘ > sin²Θ

(C) sinΘ < sin²Θ

(D) sinΘ = sin²Θ

Question 10. If ∠ A and ∠ B are complementary to each other, then the value of sec² A + sec²B – sec²
A . sec² B is

(A) 2

(B) 1

(C) 0

(D) -1

Question 11. sin²5° + sin²10° + sin²15° + …. + sin²85° + sin²90° is equal to

(A) 9

(B)  7 1/2
(C) 8 1/2

(D) 9 1/2

Question 12. In circular measure, the value of the angle 11°15′ is ?

(A) π^c/16

(B) π^c/8

(C) π^c/12

(D) π^c/4

Question 13. If 0° < Θ < 90°, the value of sin Θ + cos Θ is

(A) less than 1

(B) equal to 2

(C) equal to 1

(D) greater than 1

Question 14. The value of (tan35° tan45° tan55°) is 

(A) 0

(B) 1/2

(C) 2

(D) 1

Question 15. Maximum value of (2 sin Θ + 3 cos Θ) is 

(A) √13

(B) 2

(C) 1

(D) √15

Question 16. If sec²Θ + tan²Θ = 7, then the value of q when 0° ≤ Θ ≤ 90°, is

(A) 90°

(B) 0°

(C) 30°

(D) 60°

Question 17. If sin  + cosec Θ = 2, then the value of sin9Θ + cosec­ Θ is :

(A) 2

(B) 4

(C) 3

(D) 1

Question 18. If tan θ + cot θ = 2 then the value of θ is

(A) 60°

(B) 90°

(C) 45°

(D) 30°

Question 19. If cos px = x2– x +5/4, the value of x will be

(A)  0

(B) – 01

(C) 01

(D) None of the above

Question 20. Find the value of 1 – 2 sin²θ + sin⁴θ.

(A) cos⁴θ

(B) sin⁴θ

(C) sec⁴θ

(D) cosec⁴θ

Question 21. If cos Θ cosec 23° = 1, the value of Θ is

(A) 67°

(B) 63°

(C) 23°

(D) 37°

Question 22. The value of sin²65° + sin²θ25° + cos² 35° + cos² 55° is

(A) 1

(B) 1/2

(C) 0

(D) 2

Question 23. Which one of the following is true for 0° < q < 90° ?

(A) cosθ > cos²θ

(B) cosθ ≤ cos²θ

(C) cosθ ≥ cos²θ

(D) cosθ < cos²θ

Question 24. If a cos θ+ b sin θ = p and a sin θ – b cos θ = q, then the relation between a, b, p and q is

(A) a²– b²= p² – q²

(B) a + b = p + q

(C) a²+ b²= p² + q²

(D) a – b = p – q

Question 25. What is the measure of the central angle of the arc whose length is 11 cm and radius of the circle is 14 cm?

(A) 90°

(B) 45°

(C) 60°

(D) 75°